度量学习之对比损失
Hadsell R, Chopra S, LeCun Y. Dimensionality reduction by learning an invariant mapping[C]//2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06). IEEE, 2006, 2: 1735-1742.
这篇论文早在2006年就被提出来,其中最重要的核心思想就是减小类内距离,扩大类间距离。因此作者提出一个对比损失(contrastive loss)函数:
$$
L(W,Y,\vec{X_1},\vec{X_2})=(1-Y)\frac{1}{2}{(D_W)}^2+(Y)\frac{1}{2}{(\max{0,m-D_W})}^2
$$
其中,
$$
D_{W}(\vec{X_1},\vec{X_2})={\left|G_W(\vec{X_1})-G_W(\vec{X_2})\right|}_2
$$
这个损失函数其实可以当做两部分来看,第一部分是当$\vec{X_1}$与$\vec{X_2}$的分类或者标签又或者是身份相同时$Y=0$,此时的函数就变成了,
$$
L_S(W,\vec{X_1},\vec{X_2})=\frac{1}{2}{(D_W)}^2
$$
此时$\vec{X_1}$与$\vec{X_2}$的距离越小损失函数越小,否则当$\vec{X_1}$与$\vec{X_2}$的分类不同时$Y=1$,那么此时的函数可以看做成,
$$
L_D(W,\vec{X_1},\vec{X_2})=\frac{1}{2}{(max{ 0,m-D_W })}^2
$$
此时$\vec{X_1}$与$\vec{X_2}$的距离越大损失函数越小。下图可以很好地表示Loss值与$D_W$的关系,其中蓝色的线表示$Y=1$时的损失变化曲线,红色的线表示$Y=0$时的损失变化曲线:
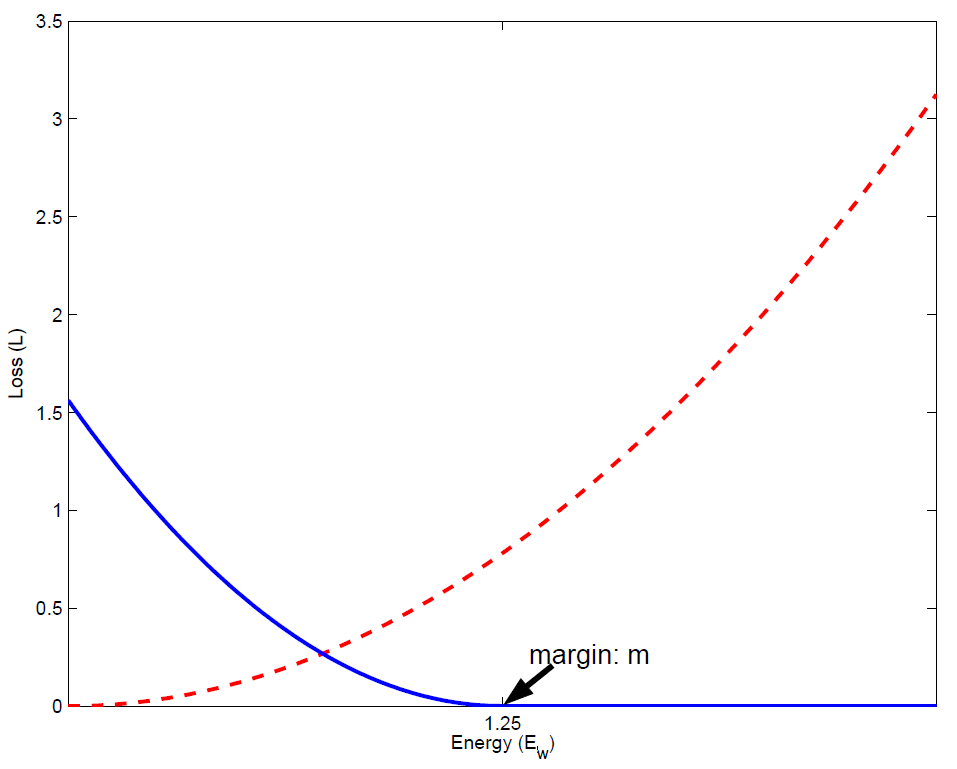
通过这种方式,对模型进行训练,就会使得模型中同一类的特征相互吸引,不同类的特征相互排斥,最后达到不同类之间的距离均大于同类之间的距离。以下是该算法应用在MNIST手写数字识别数据集上的可视化效果图:


